机器学习 lecture1 基本概念
台大李宏毅老师的机器学习课程学习笔记
视频资源:BV1Wv411h7kN
机器学习的定义
机器学习:让机器具备寻找“函数”的能力
eg:语音识别、图片识别,找到一个“对应”
“函数”的分类
回归 regression:输出是数值(scalar)的函数,输入可以是一些相关的指数
分类 classification:从给定的类别中选择并输出类别
alphago本质上是分类问题
structured learning:创造结构化的新内容
简单机器学习的步骤
写出带有未知参数的函数
$y=b+wx_{1}\ \ ···\ model$
$\\ x, y\ \ ···\ feature$
$\\ w\ \ ···\ weight$
$\\ b\ \ ···\ bias$- based on domain knowledge
- $w$ 和 $b$ 就是未知参数
通过训练数据定义损失函数
loss is a function of parameters
常见的损失函数
$L=\frac{1}{N}\sum\limits_{n}e_{n}$
$e=|y-\hat{y}|\ \ ···\ MAE$
$e={(y-\hat{y})}^{2}\ \ ···\ MSE$
$y$ 和 $\^{y}$ 是概率时使用交叉熵
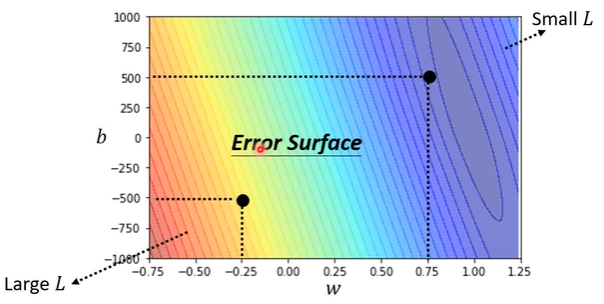
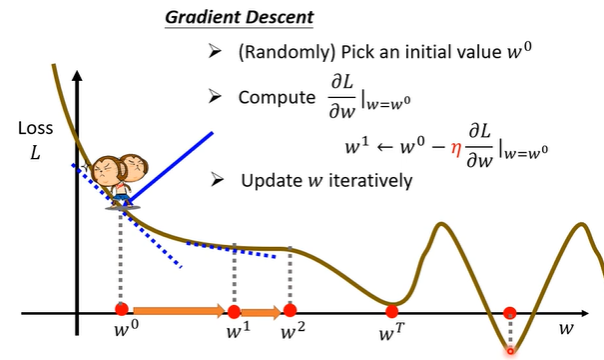
最佳化——梯度下降法
$w^{*}, b^{*} = arg \min\limits_{w,b}L$
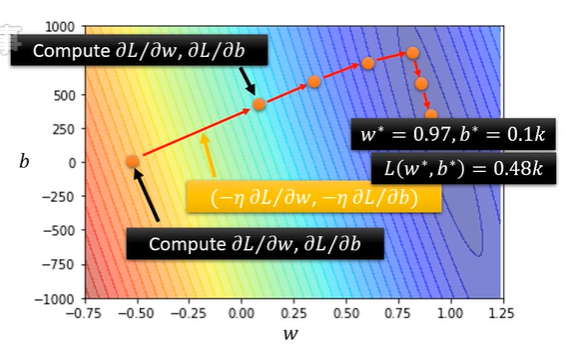
存在全局最优和局部最优的问题(但其实无关紧要——“does local minima truly cause the problem?”)
深度学习:更复杂的情况
model bias:linear models are too simple… we need more sophiscated models
如何拟合复杂的曲线函数?
通过一个常数与多个简单折线和来进行拟合,就可以拟合较为复杂的折线(piecewise linear curve)
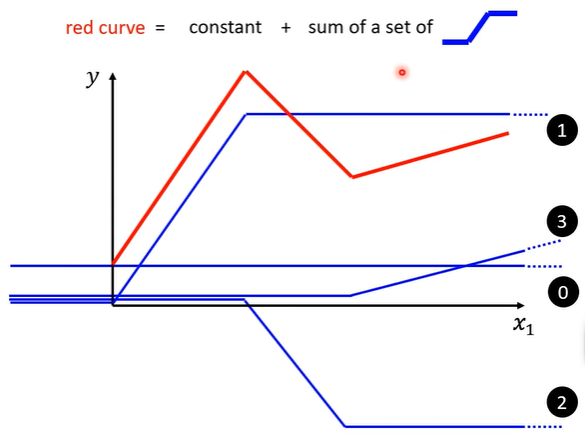
而任何复杂的曲线都可以用若干的分段线性函数来拟合。
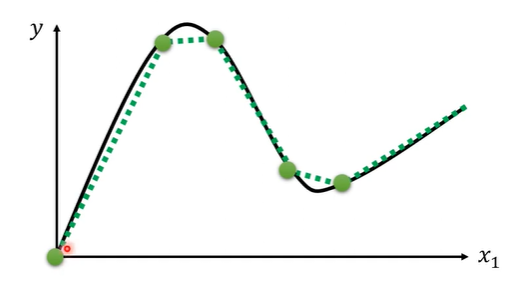
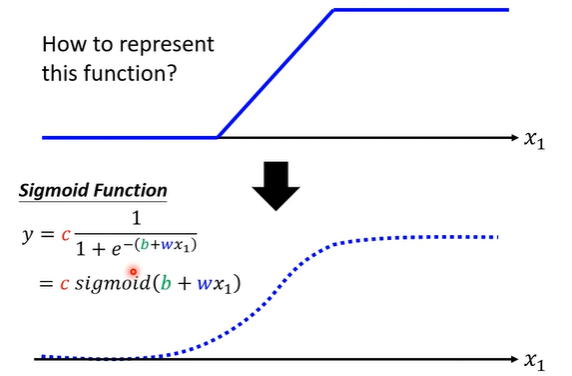
那如何表示简单折线?(称简单函数为激活函数)
使用sigmoid函数来拟合。
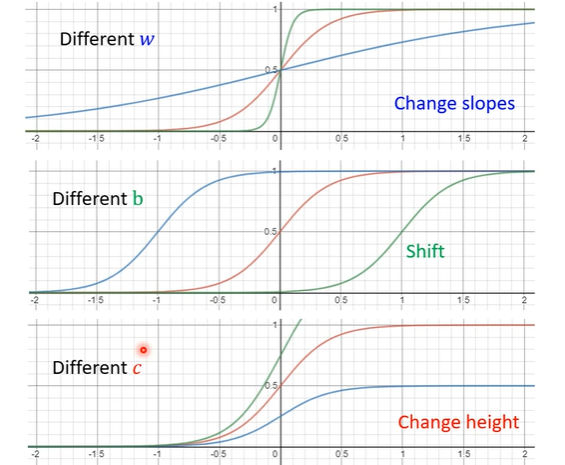
通过调整sigmoid函数的参数就可以改变简单折线的形状。
最终……
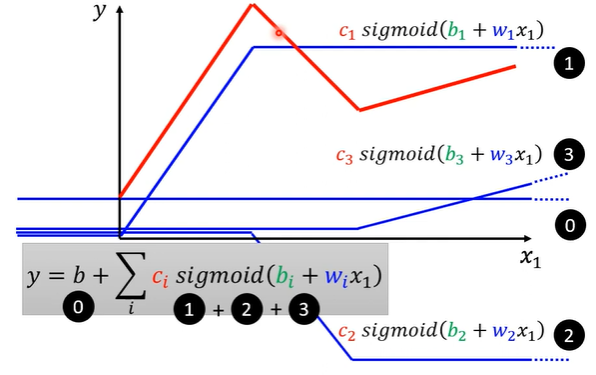
深度学习步骤
写出带有位置参数的函数
$y = b + \sum\limits_{i}c_{i}\ sigmoid(b_{i}+\sum\limits_{j}w_{ij}x{i})$,用图像表示后结合线代化简得:
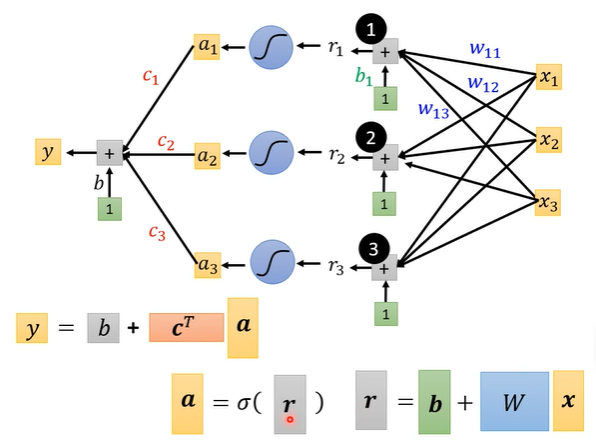
由于使用多条sigmoid曲线对原曲线进行拟合,因此黑色层有多个节点,每个节点对应一条简单曲线;每条简单曲线反映的是y和所有x之间的关系(无法用二维平面内的曲线表示了,因为这里有多个自变量x),因此每个黑色节点会连接所有的x节点。
向量形式的表示:
$y = b + \textbf{c}^{T} \sigma(\textbf{b} +\textbf{W}\textbf{x})$
$\textbf{x}(向量)\ \ ···\ feature$
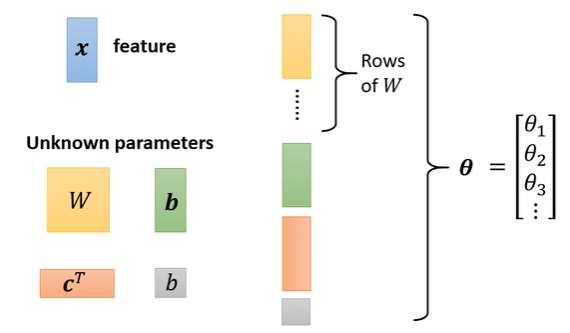
$\textbf{c}^{T}(向量),\textbf{b}(向量),\textbf{W}(矩阵)\ \ ···\ unknown\ parameters$还有一个没看懂的地方——$\theta$到底是啥啊
通过训练数据定义损失函数
$L(\theta)$,其中$\theta$表示所有位置参数的组合
最佳化(反向传播)
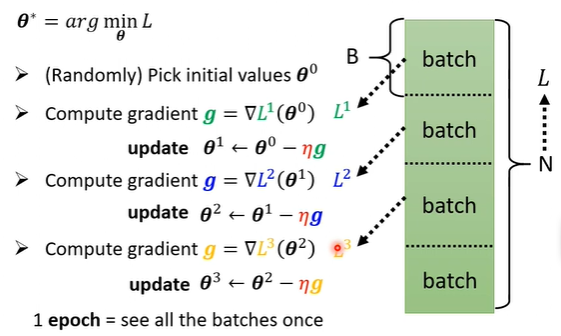
$\theta^{*} = arg \min\limits_{\theta}L$
由于这里的$\theta$真的变成了多元函数,所以求出的偏导向量也就真的变成了“梯度”用以下降:
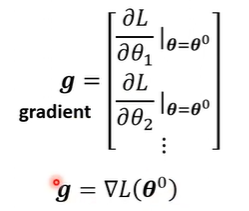
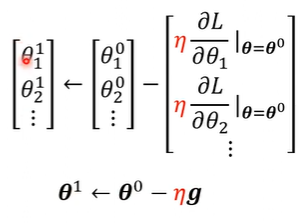
实际操作的时候,每次迭代计算损失函数的时候不会使用所有的样本数据,而是把大量数据分割成小块的数据(batch),每个batch迭代一次,完成一轮遍历后记为一个epoch,一个epoch中有多少次迭代也是手动设置的超参
再复杂一点……
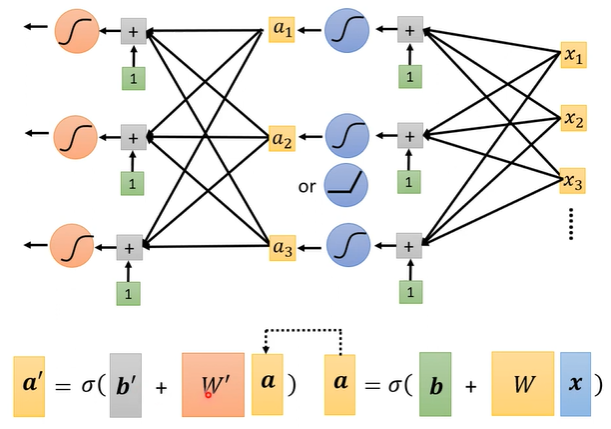
- 增加层数即可(层数也是超参 xs)
Yeah, it’s not fancy enough
所以起一个炫酷的名字:
神经网络
然而神经网络也被玩烂了怎么办捏?
那就叫深度学习吧。
下课!